动态规划入门
本篇文章是 D瓜哥 读《算法导论》的读书笔记。记录下来是为了方便整理思路,以便啃下“动态规划”这块骨头。 目前侧重记录书中关于“动态规划原理”的介绍。接下来会把书中的例子结合 Java 代码演绎一遍。后续会根据D瓜哥的学习和理解,逐步完善。最终希望达到通过这一篇文章,就能学会、理解动态规划。 山高水远,道阻且长,愿一起努力! — 2020年01月23日 |
动态规划(dynamic programming)与分治方法相似,都是通过组合子问题的解来求解原问题(在这里,“programming”指的是一种表格法,并非编写计算机程序)。
分治方法将问题划分为互不相交的子问题,递归地求解子问题,再将它们的解组合起来,求出原问题的解。
动态规划应用于子问题重叠的情况,即不同的子问题具有公共的子子问题(子问题的求解是递归进行的,将其划分为更小的子子问题)。
在这种情况下,分治算法会做许多不必要的工作,它会反复地求解那些公共子问题。
动态规划算法对每个子子问题只求解一次,将其解保存在一个表格中,从而无需每次求解一个子子问题时都重新计算,避免了不必要的计算工作。
动态规划方法通常用来求解最优化问题(optimization problem)。
设计一个动态规划算法的步骤:
刻画一个最优解的结构特征。
递归地定义最优解的值。
计算最优解的值,通常采用自底向上的方法。
利用计算出的信息构造一个最优解。
算法原理
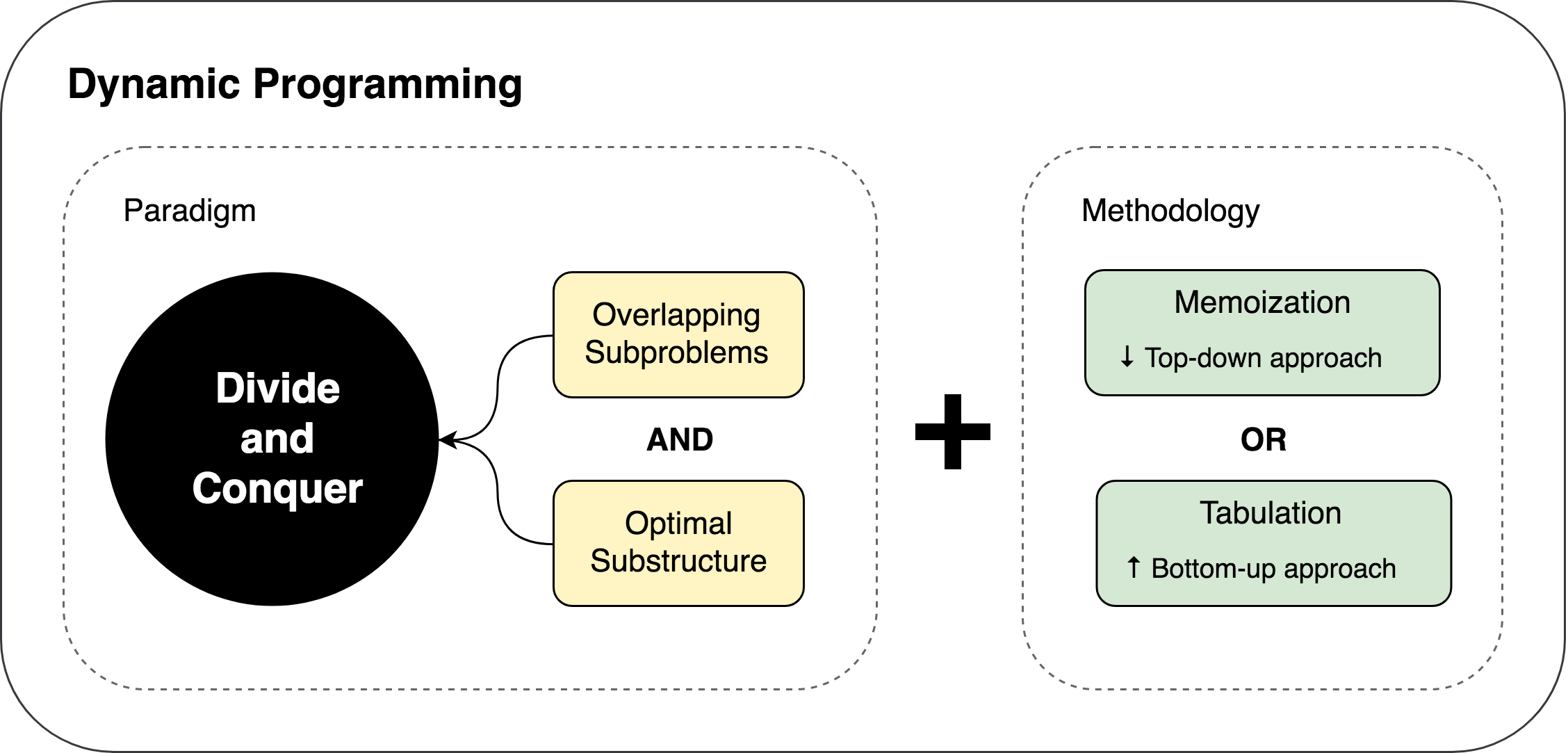
适合应用动态规划方法求解的最优化问题应该具备的两个要素:最优子结构和子问题重叠。
最优子结构
用动态规划方法求解最优化问题的第一步就是刻画最优解的结构。如果一个问题的最优解包含其子问题的最优解,则称此问题具有最优子结构性质。因此,某个问题是否适合应用动态规划算法,它是否具有最优子结构性质是一个好线索。
发掘最优子结构性质的通过模式
证明问题最优解的第一个组成部分是做出一个选择。做出这次选择会产生一个或多个待解的子问题。
对于一个给定问题,在其可能的第一步选择中,你假定已经知道哪种选择才会得到最优解。你现在并不关心这种选择具体是如何得到的,只是假定已经知道了这种选择。
给定可获得最优解的选择后,你确定这次选择会产生哪些子问题,以及如何最好地刻画子问题空间。
利用“剪切-粘贴”(cut-and-paste)技术证明:作为构造原问题最优解的组成部分,每个子问题的解就是它本身的最优解。证明这一点是利用反证法:假定子问题的解不是其自身的最优解,那么我们就可以从原问题的解中“剪切”掉这些非最优解,将最优解“粘贴”进去,从而得到原问题一个更优的解,这与最初的解是原问题最优解的前提假设锚段。
一个刻画子问题空间的好经验是:保持子问题空间尽可能简单,只在必要时才扩展它。
对于不同问题领域,最优子结构的不同体现在两个方面:
原问题的最优解中涉及多少个子问题,以及
在确定最优解使用哪些子问题时,我们需要考察多少种选择。
可以用子问题的总数和每个子问题需要考察多少种选择这两个因素的乘积来粗略分析动态规划算法的运行时间。
在动态规划方法中,通常自底向上地使用最优子结构。也就是说,首先求得子问题的最优解,然后求原问题的最优解。在求解原问题过程中,我们需要在涉及的子问题中做出选择,选出能得到原问题最优解的子问题。原问题最优解的代价通常就是子问题最优解的代价加上由此次选择直接产生的代价。
能够使用贪心算法的问题也必须具有最优子结构性质。贪心算法和动态规划最大的不同在于,它并不是首先寻找子问题的最优解,然后在其中进行选择,而是首先做出一次“贪心”选择—在当时(局部)看来最优的选择—然后求解选出的子问题,从而不必费心求解所有可能相关的子问题。
| 问题:使用贪心算法和动态规划的界线是什么?什么时候使用贪心?什么时候使用动态规划? |
重叠子问题
适合用动态规划方法求解的最优化问题应该具备的第二个性质是子问题空间必须足够“小”,即问题的递归算法会反复地求解相同的子问题,而不是一直生成新的子问题。
如果递归算法反复求解相关的子问题,则就称为最优化问题具有重叠子问题(overlapping subproblems)性质。
与之相对的,适合用分治算法求解的问题通常在递归的每一步都生成全新的子问题。
动态规划算法通常这样利用重叠子问题性质:对每个子问题求解一次,将解存入一个表中,当再次需要这个子问题时直接查表,每次查表的代价为常量时间。
一个问题是否适合用动态规划求解同事依赖于子问题的无关性和重叠性。两个子问题如果不共享资源,它们就是独立的。而重叠是指两个子问题实际上是同一个子问题,只是作为不同问题的子问题出现而已。
将自顶向下的递归算法(无备忘录)与自底向上的动态规划算法进行比较,后者要高效得多,因为它利用了重叠子问题性质。
重构最优解
从实际考虑,通常将每个子问题所做的选择存在一个表中,这样就不必根据代价来重构这些信息。
备忘
可以保持自顶向下策略,同时达到与自底向上动态规划方法相似的效率。思路就是对自然但低效的递归算法加入备忘机制。维护一个表记录子问题的解,但仍然保持递归算法的控制流程。
带备忘的递归算法为每个子问题维护一个表项来保存它的解。每个表项的初值设为一个特殊值,表示尚未填入子问题的解。当递归调用过程中第一次额遇到子问题时,计算其解,并存入对应表项。随后每次遇到同一个问题,只是简单地查表,返回其解。
| 一个更通用的备忘方法是使用散列技术,以子问题参数为关键字。 |
通常情况下,如果每个子问题都必须至少求解一次,自底向上动态规划算法会比自顶向下备忘算法快,因为自底向上算法没有递归调用的开销,表的维护开销也更小。而且,对于某些问题,可以利用表的访问模式来进一步降低时空代价。相反,如果子问题空间中的某些子问题完全不必求解,备忘方法就会体现出优势了,因为它只会求解那些绝对必要的子问题。